One can solve an equation using a scale. In the example below, an unknown weight is wrapped in aluminum paper. Known weights are shown in the scale. First, one can write down the equation. The unknown is x. The sum of the weights in the first dish of the scale equals the sum of the weights in the second dish because the scale is balanced.
One can apply 2 rules to find the value of x: 1) one can remove similar weights from both dishes because the scale remains balanced; 2) one can split a weight on one dish of the scale by smaller weights that add up to the original weight.
Using these rules one can solve, for example, x+3=10. First, one splits the 10 on the second dish to obtain x+3=5+3+2. Second, one removes the weights 3 on both dishes to obtain x=5+2. Therefore, x=7. When an equation includes a “negative weight”, we need to put that weight in the dish on side of the scale. For example, to translate the equation x+2-5=10 to the scale, we need to put weights x and 2 in the first dish of the scale and weights 10 and 5 in the second dish of the scale.


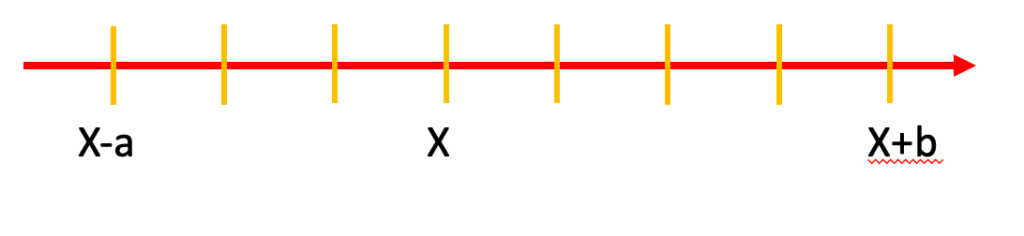
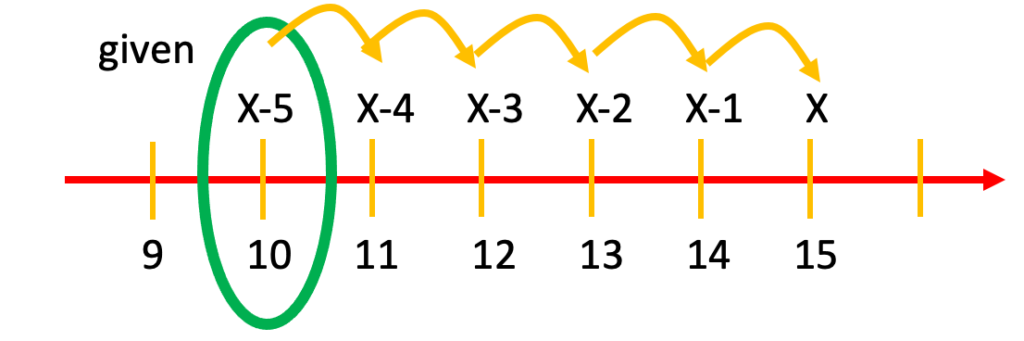
One can also use the number line to solve equations. We need to know where x is when x-a is given and where x is when x+b is given. For example, if x-5 is given, x is 5 units to the right of it. If x+3 is given, x is 3 units to the left of it.
Using the number line, one can solve, for example, x-5=10. One can also solve, for example, x+3=10. One can solve 10=x-2 by reading from right to left, x-2=10. Likewise, for solving 9=x+4. One can also solve, for example, 3+x=10, by writing x+3=10. The more complicated case is solving, for example, 10-x=2. In this case, one must add x to both sides to get 10=2+x.

We can solve two equations using two scales to find x and y. In the example below, two unknown weights are wrapped in aluminum paper with different colors. In this case, a third rule can be used: 3) one can substitute an unknown for whatever weight it amounts to from one scale to the other.
For example, imagine we want to solve x+y=10 and x+3=5+y. We start by splitting the 5 in the second dish of the second scale to obtain x+3=3+2+y. Then we remove the weight 3 on both dishes of this scale to obtain x=2+y. Then we substitute x in the first dish of the first scale by the weights 2 and y to obtain 2+y+y=10. Then we split the weight 10 in this scale to obtain 2+y+y=2+3+5. Then we remove the weight 2 on both dishes of this scale to obtain y+y=3+5. That is, y+y=8. Therefore, y=4. Then we substitute y for weight 4 in the second scale to obtain x=2+4. Therefore, x=6. Here are these steps in practice:

